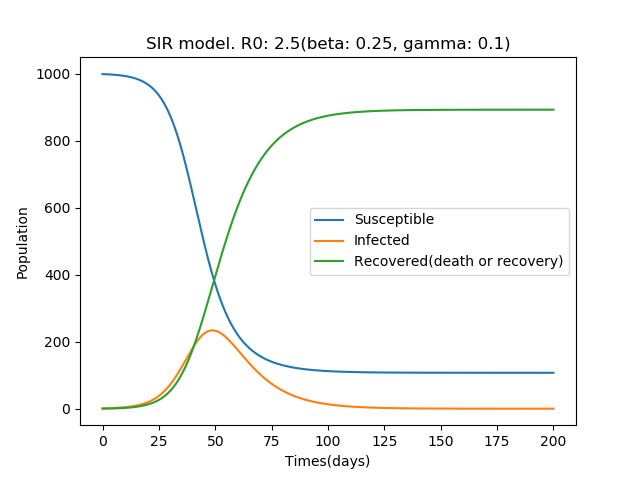
感染症流行の数理(SIRモデル)のグラフ化
お久しぶりです。ブログ更新サボっていました(^_^;) 3月頃からの新型コロナウイルスのパンデミックにより、世界中が混乱に陥っていますね。私も日々ニュースをみて不安になったり、投資の含み損を見て嫌な気持ちになったりしています。 仕事もフルリモートワークとなって、オーバワーク気味で疲れが溜まっておりました。しかし、ゴールデンウィークの休みで元気を取り戻してきました。 今回の記事は気分転換とリハビリも兼ねて、雑記回です。コロナショックで不安を抱えている方への頭の体操や、プログラミングの入門となれば幸いです。 さて、今回は感染症流行の古典的モデルである「SIRモデル」をPythonでプログラミングしてみました。 SIRモデルは、すでに色々なサイトやYoutubeで解説されておりますが、感染症の流行を表すのに一番シンプルな数学的なモデルだそうです。100年近く前からあるモデルですが、未だに使えるそうです。SIRモデルの詳しい数理は Wikipedia や後述の参考サイトに解説があるので、興味のある方は調べてみると面白いと思います。 基本再生算数2.5のときのグラフ SIRモデルにおいて、感染率βを0.25、回復率γを0.1(10日間で隔離、回復または死亡する)、つまり1人の感染者が感染を移す人数R0(基本再生算数)を2.5とした場合の流行は以下のようなグラフとなりました。 R0=2.5という数字は、専門家会議で提示されていたものです。実態はまだわからないそうですが、2~3くらいというのが見立てだそうです。 感染者が発生してから流行のピークまで約50日ほどかかり、20%以上の方が感染し、流行収束までに約90%が感染するとなりました。 日本では、重症者だけ受け入れるとしても、医療キャパシティはせいぜい数千から数万人程度でしょうから、 ほとんどの人が軽症とはいえ、放っておけば医療崩壊待ったなしですね。 再生算数を低く抑えながらみんなの免疫がつくまで長く付き合っていかざるをえなさそうですね。 SIRモデルのソースコード(Python) グラフを表示するのに使ったPythonのソースコードです。参考サイトのものをほとんどコピーしたものですが、一部見やすく修正しています。差分方程式を解いたり、グラフ化したりするのにこんな短いコードでできるとは、素晴らしいですね。 Pythonはほとんど使ったことがないのですが、使いやすいですね。世界中で流行しているのもうなずけます。 import numpy as np from scipy.integrate import odeint from scipy.optimize import minimize import matplotlib.pyplot as plt # the effective contact rate of the disease BETA = 0.25 # recovery rate GAMMA = 0.1 R_nought = BETA / GAMMA # max time(days) MAX_DAYS = 200 # delta time DT = 0.01 # Number of population NUM_POPULATION = 1000 # Initial infected population I_INIT = 1 # Initial susceptible population S_INIT = NUM_POPULATION - I_INIT # Initial removed population (either by death or recovery) R_INIT = 0 # SIR Differential Equation def diff_eq_func(y, time, NUM_POPULATION, BETA, GAMMA): susceptible = y[0] infectious = y[1] ds_dt = -BETA * susceptible * infectious / NUM_POPULATION di_dt = BETA * susceptible * infectious / NUM_POPULATION - GAMMA * infectious dr_dt = GAMMA * infectious return [ds_dt, di_dt, dr_dt] # Solver SIR model y_init = [S_INIT, I_INIT, R_INIT] times = np.arange(0, MAX_DAYS, DT) result = odeint(diff_eq_func, y_init, times, args=(NUM_POPULATION, BETA, GAMMA)) # plot plt.plot(times, result) plt.title('SIR model. R0: ' + str(R_nought) + '(beta: ' + str(BETA) + ', gamma: ' + str(GAMMA) + ')') plt.legend(['Susceptible', 'Infected', 'Recovered\n(isolated/death/recovery)']) plt.xlabel('Time(days)') plt.ylabel('Population') plt.show() 参考サイト Wikipedia ...